2025年7月期の過去問
▶2025年7月の第1週の問題

【問題】
テーブルに10枚のコインが並んでいます。表向きのコインが5枚、裏向きが5枚あります。あなたは目隠しをしているためコインの向きを目で区別できません。しかし、コインを2つの山に分け、どちらの山も同じ数の表向きコインを含むようにしたいと考えています。コインを見ずにどうすればこの条件を満たせるでしょうか?
【答え】
1.テーブル上のコインから任意に5枚を取り、これを「山A」とする。
2.山Aの5枚すべてを裏表ひっくり返す。
これで、「山A」と残りの「山B」は、それぞれ同じ枚数の表向きコインを持つことになります。
▶2025年7月の第2週の問題
【問題】
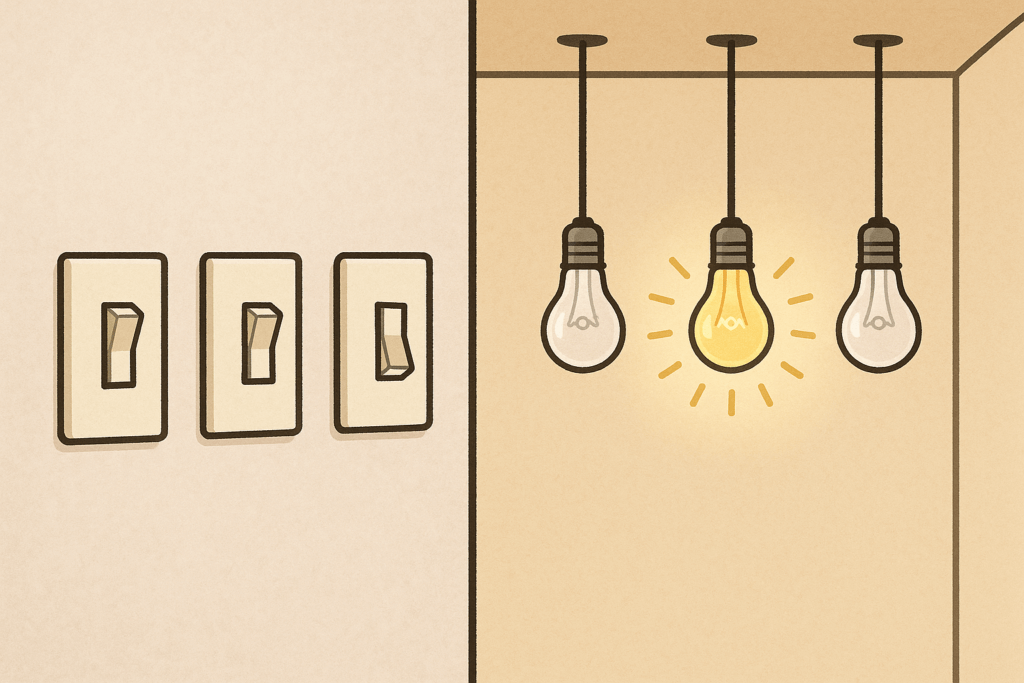
あなたは、部屋の外にある3つのスイッチと、部屋の中にある3つの電球を操作しなければなりません。
・スイッチはそれぞれ対応する電球をオン/オフにします。
・部屋には一度だけ入ることが許されています。
・スイッチの操作は部屋の外でしかできません。
どうすれば、どのスイッチがどの電球を操作しているかを正確に見分けられるでしょうか?
【答え】
最初にスイッチ①を「オン」にし、しばらく(約5分)待つ。
スイッチ①を「オフ」にして、すぐにスイッチ②を「オン」にする。
そのまま部屋に入り、3つの電球を調べる。
・点灯していれば → スイッチ②が対応
・消えていて熱いもの → 最初にオンにして熱くなったが、後でオフにしたスイッチ①が対応
・消えていて冷たいもの → 一度もオンにされなかったスイッチ③が対応
▶2025年7月の第3週の問題

【問題】
ある農夫が狼、ヤギ、キャベツを連れて川を渡ろうとしています。小舟は農夫と一度に1つのものしか運べません。また、次のルールがあります:
・狼とヤギだけを岸に残すと、狼がヤギを食べてしまう。
・ヤギとキャベツだけを岸に残すと、ヤギがキャベツを食べてしまう。
どのようにすれば、農夫・狼・ヤギ・キャベツをすべて無事に向こう岸へ渡せるでしょうか?
【答え】
1.農夫がヤギを連れて向こう岸へ渡す。
2.農夫は小舟だけを持って戻る。
3.農夫がキャベツを連れて向こう岸へ渡す。
4.農夫がヤギを連れて手前岸へ戻る。
5.農夫が狼を連れて向こう岸へ渡す。
6.農夫は小舟だけを持って戻る。
7.再び農夫がヤギを連れて向こう岸へ渡す。
以上の手順で、どの時点でも危険な組み合わせを作らずに全員を渡せます。
▶2025年7月の第4週の問題

【問題】
夜、吊り橋を渡らなければならない4人がいます。4人は吊り橋を渡りきるのに、それぞれ以下の時間が掛かります。
・アリス:1分
・ボブ:2分
・キャロル:7分
・デイブ:10分
吊り橋は一度に2人までしか渡れず、一つしかない懐中電灯を持つ為の人は必ず同行しなければなりません。全員を17分以内で向こう岸へ渡らせるには、どのように進めればよいでしょうか?
【答え】
1.アリス(1分)とボブ(2分)が懐中電灯を持って渡る(所要時間:2分)。
2.アリスが懐中電灯を持って戻る(所要時間:1分)。
3.キャロル(7分)とデイブ(10分)が懐中電灯を持って渡る(所要時間:10分)。
4.ボブが懐中電灯を持って戻る(所要時間:2分)。
5.アリスとボブが懐中電灯を持って渡る(所要時間:2分)。
合計:2 + 1 + 10 + 2 + 2 = 17分で、全員が渡り切れます。
▶2025年7月の第5週の問題

【問題】
テーブルに3つの箱があります。
・箱Aにはリンゴのみ
・箱Bにはオレンジのみ
・箱Cにはリンゴとオレンジの混合
という中身ですが、箱にはそれぞれ「リンゴのみ」「オレンジのみ」「混合」とラベルが貼られており、どのラベルも必ず間違っています。
あなたは中を覗くことはできませんが、1回だけ任意の箱から果物を1つ取り出すことができます。
この1回の取り出しだけを使って、すべての箱に正しいラベルを貼り直すにはどうすればよいでしょうか?
【答え】
1.「混合」とラベルが貼られた箱から果物を1つ取り出す。
・もし取り出したのがリンゴなら、その箱は「リンゴのみ」。
・もし取り出したのがオレンジなら、その箱は「オレンジのみ」。
2.残る2つの箱は、どちらもラベルが間違っているので、
・1でもしリンゴ箱とわかった場合、箱に元々付いていたラベル(混合)を剥がし、正しく「リンゴのみ」と貼り替える。
・残った2箱は、「リンゴのみ」「オレンジのみ」のラベルが付いていたはずだが、それぞれ逆なので、「リンゴのみ」となっていた箱は実際にオレンジのみ→正しく「オレンジのみ」
そして残った箱が自動的に「混合」となる。
2025年8月期の過去問
▶2025年8月の第1週の問題

【問題】
3人の囚人A、B、Cが一列に並んでいます。
・帽子は合計5つあり、「白」が3つ、「黒」が2つ。
・その中からランダムに3つをA・B・Cにかぶせ、残り2つは見えないようにする。
・AはBとCの帽子が見える。BはCの帽子が見える。Cは誰の帽子も見えない。
看守が順に問いかけます。
1.看守:「Aさん、あなたの帽子の色は何色?」
A:「わかりません。」
2.看守:「Bさん、あなたの帽子の色は何色?」
B:「わかりません。」
3.看守:「Cさん、あなたの帽子の色は何色?」
Cは自分の帽子の色を当てることができます。さて、Cの帽子は何色でしょうか?
【答え】
Cの帽子は「白」です。
【解説】
1.Aが「わからない」と答えた時点で、AはBとCが両方とも黒ではなかったことがわかります。
・Aが黒×2を見れば残りは白×3、Aは「白」と即断できるため。
2.それを聞いてBは、「自分とCが両方黒ではない」ことを前提に、自分の帽子を推理します。
・BがCを見て黒だった場合、BとCが両方が黒であればAはわかったはずなので、Bは「自分は白」と即決できます。
・しかしBは「わからない」と答えたので、Cは黒ではなく白だとわかります。
3.以上より、Cは自分の帽子が「白」であると断定できます。
▶2025年8月の第2週の問題
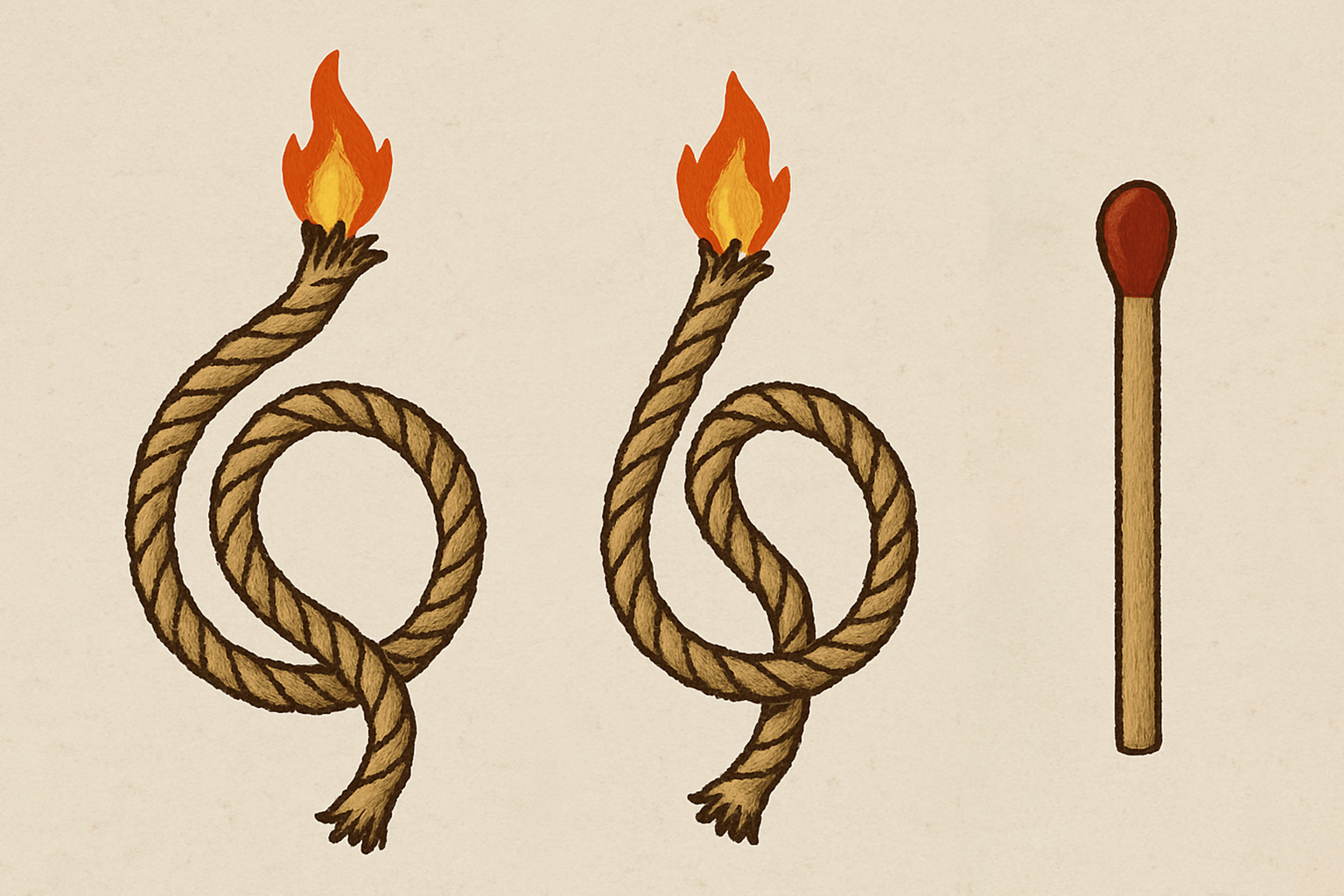
【問題】
あなたは不規則に燃えるロープを2本持っています。
・どちらのロープも、先端から着火するとちょうど1時間で燃え尽きますが、燃え方は一定ではありません(ロープの長さや途中の太さに関わらず、燃焼速度は場所によって変わります)。
・あなたはマッチを1本しか持っておらず、ロープは先端や両端など、好きな位置から着火できます。
【答え】
1.ロープAを両端から同時に着火し、ロープBを片端だけ着火する。
2.ロープAが燃え尽きた時点で、必ず30分経過している。
3.その瞬間にロープBのもう一方の端にも着火する(これでロープBは両端から燃え始める)。
4.残ったロープBは両端から燃えるため、残りの燃焼に15分かかる。
5.よって、ロープBが燃え尽きた時点で、合計45分が正確に経過している。
▶2025年8月の第3週の問題

【問題】
ある城には2つの扉があります。
・1つは「自由への扉」、もう1つは「死への扉」です。
・この扉を守る守衛が2人いて、1人は必ず真実を話し、もう1人は必ず嘘をつきます。
・どちらが真実を話す守衛かはわかりません。
あなたはどちらか1人の守衛に、質問を一度だけできることになっています。
この質問だけで、どちらの扉が自由への扉かを確実に見分けるには、何と質問すればよいでしょうか?
【答え】
守衛のどちらか一人に以下の質問をします。
「もしもう一方の守衛に『この扉は自由への扉ですか?』と尋ねたら、彼は何と答えますか?」
・もしその守衛が「はい」と答えたら――
→ その扉は自由への扉ではありません。
・もし「いいえ」と答えたら――
→ その扉が自由への扉です。
この質問によって、真実を話す守衛でも嘘をつく守衛でも、必ず「自由への扉ではない」と答えが返ってくる扉がわかるため、反対側を選べば必ず自由への扉にたどり着けます。
▶2025年8月の第4週の問題
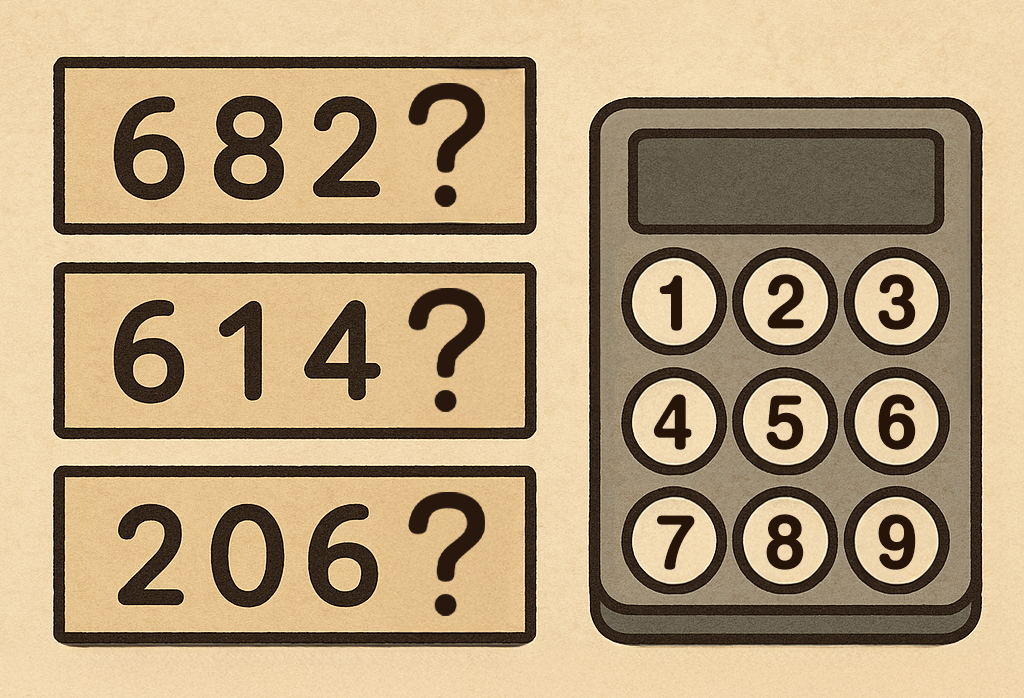
【問題】
以下のヒントが与えられている時、3桁の暗証番号を解読せよ。
・682 → 1つの数字が合っていて、正しい位置にある
・614 → 1つの数字が合っているが、位置が違う
・206 → 2つの数字が合っているが、両方とも位置が違う
・738 → 全ての数字が間違っている
・780 → 1つの数字が合っているが、位置が違う
【答え】
暗証番号は 042 です。
【解説】
1.ヒント「738」で 7, 3, 8 は全て不使用とわかる。
2.ヒント「682」で 8 は使えないので、「6」「2」のいずれかが正しく、位置も合っている。
・もし「6」が先頭にあれば、ヒント「206」で 6 は位置が違う数字として数えられるはずだが、ここでは「正しい位置」にある候補としてカウントできないため矛盾。
・よって「2」が末尾(正しい位置)であると確定。
3.ヒント「206」で「2」は末尾にあるため①の“位置違い”としてカウントされる。残り1つは {0, 6} のうちどちらか。
・もし「6」を含むなら「6」は末尾(位置違い)でもう一度カウントされるが、「6」を含む場合、ヒント「614」で正しく1つしかヒットしない条件を満たせない。
・よって「0」が含まれ、位置は原典(206の2番目)とは異なるはず →「0」は先頭へ。
4.以上より残る中央の数字はヒント「614」のうちの「4」。
・ヒント「614」では「4」は3番目にあるが、ここでは2番目に置くことで“位置違い”の条件を満たす。
・ヒント「780」でも「0」は3番目→1番目に移動させて“位置違い”としてカウントされる。
以上から、正しい暗証番号は 042 となります。
2025年9月期の過去問
▶2025年9月の第1週の問題

【問題】
城の廊下に5つの扉があります。1つだけが宝物庫への扉で、他は行き止まりです。各扉には下記の看板がかかっています。
1.「宝物庫は扉①または②のどちらかにある」
2.「宝物庫は扉②ではない」
3.「宝物庫は奇数番の扉にある」
4.「宝物庫は扉④ではない」
5.「宝物庫は扉③または⑤のどちらかにある」
看板のうち、ちょうど2つだけが真実で、残り3つは偽りです。
さて、宝物庫への扉はどれでしょうか?
【答えと解説】
各看板の真偽を判定し、「真」は1点、「偽」は0点とします。最終的に合計点がちょうど2点になる扉が正解です。
①〇〇〇〇✕ 4点
②〇✕✕〇✕ 2点
③✕〇〇〇〇 4点
④✕〇✕✕✕ 1点
⑤✕〇〇〇〇 4点
•扉② の場合のみ、ちょうど2つの看板だけが「真」となり、残り3つが「偽」になります。
•他の扉を仮定すると、「真」の数が2以外(1, 4)となってしまうため、条件を満たしません。
以上より、宝物庫への扉は 扉② であると確定します。
▶2025年9月の第2週の問題
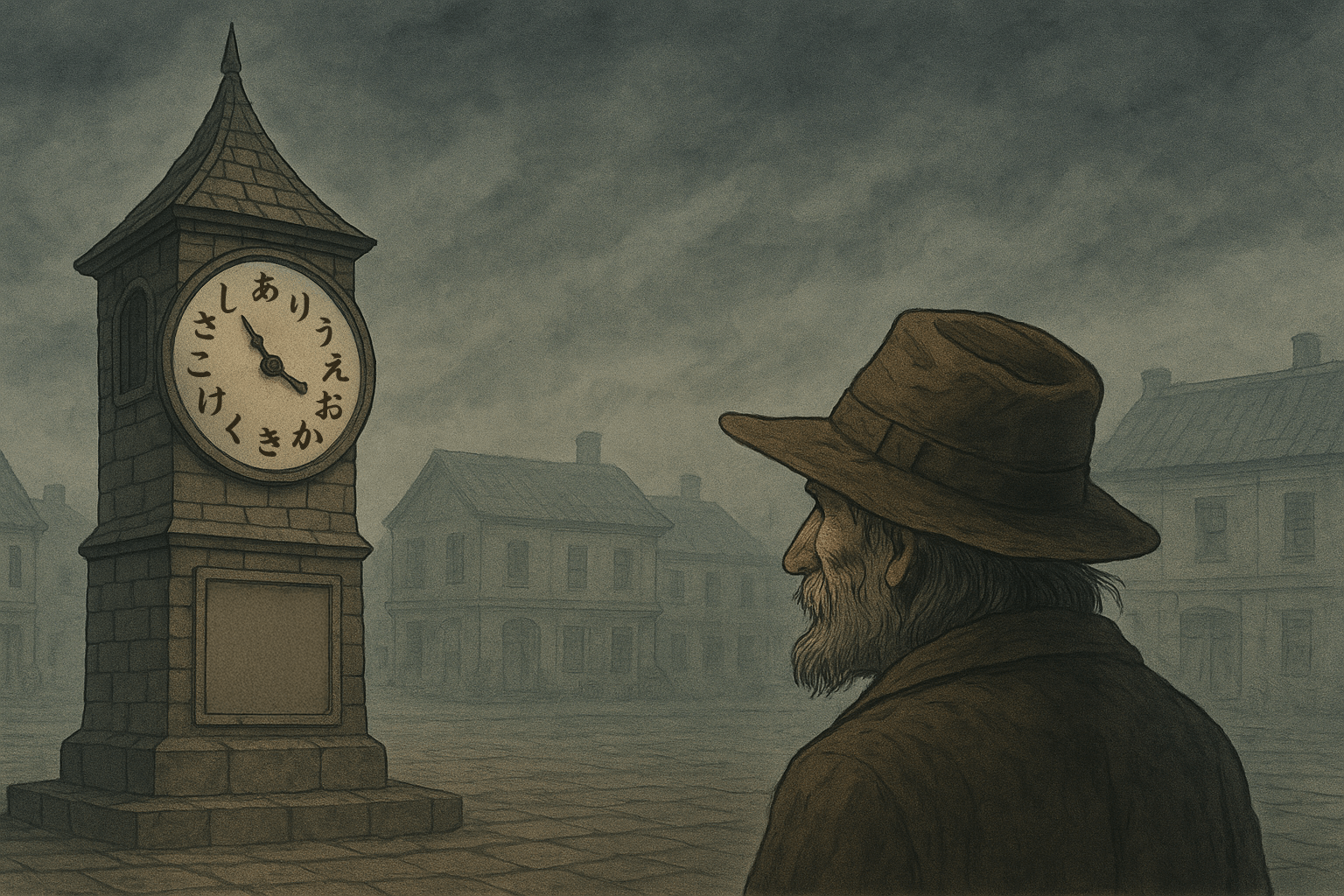
【問題】ある霧深い町を訪れた旅人。町の広場には、時を刻むのをやめて久しい、古びた時計塔が静かに佇んでいた。文字盤には数字の代わりに、不思議なひらがなが並んでいる。
町の老人曰く、「あの時計が示す『真実の時刻』を解き明かせた者だけが、町の宝を手にできるのじゃ」と。
時計塔の文字盤には、12時の位置から時計回りに、次の12文字が記されている。
あ、り、う、え、お、か、き、く、け、こ、さ、し
そして、時計塔の足元にある石板には、こう刻まれていた。
「針が重なり、再び重なるまでの間に、 短き針が指し示す、ただ一つの母音。 それが、宝への扉を開く声となる。」 さて、ナゾは解けるかな? 宝への扉を開く声、すなわち答えとなる母音一文字を答えてくれたまえ。
【答えと解説】
この謎を解く鍵は、石板に書かれた「針が重なり、再び重なるまでの間」という一文を正確に理解することにあります。
1.まず、時計の長針と短針が重なる時刻について考えます。例えば、お昼の12時ちょうどに針は重なりますね。
2.次に、そこから長針と短針が**「再び重なる」のはいつでしょうか? 多くの人は1時5分過ぎと考えますが、正確な時刻は約1時間5分27秒後、つまり約65.5分に一度のペースで重なります。12時間で11回重なる計算です。
3.重要なのは、この「針が重なってから、次に重なるまで」の約65.5分という時間です。この間に、短針(時を示す針)は文字盤の上を少しだけ進みます。
4.次に、「短き針が指し示す、ただ一つの母音」という部分に注目します。文字盤の文字をよく見てみましょう。
あ(母音)、り、う(母音)、え(母音)、お(母音)、か、き、く、け、こ、さ、し
この中に母音は「あ、う、え、お」の4つあります。
5.針が重なるのは、12時ちょうど、1時5分過ぎ、2時10分過ぎ…と続いていきます。 それぞれの重なる瞬間の「間」で、短針はどの文字の範囲を動くでしょうか?
・12時〜1時5分過ぎの間:短針は「あ」と「り」の間を指します。
・1時5分過ぎ〜2時10分過ぎの間:短針は「り」と「う」の間を指します。
・2時10分過ぎ〜3時15分過ぎの間:短針は「う」と「え」の間を指します。
・3時15分過ぎ〜4時20分過ぎの間:短針は「え」と「お」の間を指します。
おや? 2時過ぎから3時過ぎにかけての間、短針は母音である「う」のエリアを通過し、次の母音である「え」のエリアに入ってしまいます。これでは、その間に指し示す母音は「う」と「え」の二つになってしまい、「ただ一つの母音」という条件に合いません。
6.では、短針が母音を一つだけ指し示す区間はどこでしょう? それは、1時5分過ぎに針が重なり、次に2時10分過ぎに重なるまでの間です。 この約65.5分の間に、短針は「り」(子音)のエリアから始まり、「う」(母音)のエリアを通過し、次の「え」(母音)に到達する前に、長針に追いつかれます。 したがって、この期間に短針が指し示した母音は「う」ただ一つだけなのです。
よって、宝への扉を開く最初の声は「う」となります。
▶2025年9月の第3週の問題

【問題】
巨万の富を築きながらも、生涯孤独であった風変わりな資産家が亡くなった。
彼の書斎から、一枚の羊皮紙が見つかる。それは、遺産の相続人を決めるための、奇妙なテストが記された遺言状だった。
遺言状には、2つのリストが並べられている。
【空を舞える言葉】
・夕日
・気候
・想い
・用心
【地へ堕ちる言葉】
・朝日
・天気
・悩み
・堅実
そして、羊皮紙の最後は、こう締めくくられていた。
「さて、私が生涯をかけて愛し続けた『気球』は、果たしてどちらへ行くのだろうか?」
遺言に記された「空」か「地」か、
資産家の問いに、あなたならどう答えますか?
【答えと解説】
答え:空を舞う
解説:この謎の鍵は、単語の意味や文字の形ではなく、「それらの文字をどうやって入力するか」という点に隠されています。
まず、2つのリストに並んだ単語の間に、意味や文字数、母音の数といった単純な共通点がないかを探します。しかし、それらの方法では法則性を見つけることはできません。
ここで視点を大きく変える必要があります。これらのアルファベットを、私たちが普段使っているパソコンのキーボード(QWERTY配列)で入力する場面を想像してみてください。
【空を舞える言葉】のリストにある YUUHI, KIKOU, OMOI, YOUJIN は、すべて右手で打つキーだけで構成されています。(基本のポジションで Y, U, I, O, P, H, J, K, L, N, M など)
一方、【地へ堕ちる言葉】のリストにある ASAHI, TENKI, NAYAMI, KENJITSU は、すべて両手で打つキーで構成されています。
この遺言状は、キーボードの右手のみで入力できる言葉を「空」になぞらえていたのです。
▶2025年9月の第4週の問題

【問題】
あなたは昔ながらの小さな博物館の学芸員です。展示室に並んだ5つの展示ケース(左から 1番 → 5番)には、それぞれ異なる作品名と異なる素材名が付けられていました。しかし、それらは地震によりすべてバラバラになってしまいました。作品名と素材名は以下の5種類ずつで、どれも1回ずつ使われています。
作品名:太陽、波、鷹、渦巻、十字
素材名:青銅、オーク材、大理石、磁器、羊皮紙
あなたの仕事は、以下の手がかりだけを頼りに「各展示ケースにどの作品名、素材名が付いていたか」を突き止めることです。唯一の正解を導いてください。
~手がかり~
・大理石は渦巻の左側にある。ただし隣り合ってはいない。
・太陽はオーク材のすぐ右に付いている。
・鷹は端のどちらかのケースにある。
・磁器はちょうど中央のケースにある。
・青銅は羊皮紙の左側にあり、間に二つ別の作品がある。
・十字は波と隣り合っている。
・オークは大理石と隣り合っていない。
・鷹は青銅ではない。
【答えと解説】
~答え~
左から順に(作品名 / 素材名)
1番:鷹 / 大理石
2番:十字 / 青銅
3番:波 / 磁器
4番:渦巻 / オーク材
5番:太陽 / 羊皮紙
~解説~
・手がかり4で磁器は位置3と確定。
・手がかり2で太陽はオークのすぐ右と磁器が3番にあることから、オークと太陽の可能な組はオーク=2番、太陽=3番かオーク=4番、太陽=5番。しかし太陽が3番なら他の条件と合わせると矛盾するため(実際に検討すると唯一残るのはオーク=4番、太陽=5番)、4番はオーク、5番は太陽。
・手がかり5「青銅は左で、羊皮紙は青銅の右側で 3つ離れている」から、可能な組み合わせは青銅=1番 & 羊皮紙=4番、または 青銅=2番 & 羊皮紙=5番になる。ただし位置4はすでにオークなので青銅=1番、羊皮紙=4番 は不可。したがって 青銅=2番、羊皮紙=5番 が決定。
・これで2番は 青銅、5番は 羊皮紙(=太陽と同じケース)と確定。手がかり8(鷹は青銅ではない)より、鷹は2番(青銅)にはいない。手がかり3で鷹は端(1番か5番)。しかし5番は既に太陽なので鷹は1番で確定。
・手がかり1(大理石は渦巻の左で隣り合わない)と手がかり7(オークは大理石と隣り合わない)を合わせると、大理石は1番であることが矛盾なく収まる(4番にオークがあるので隣接していない)。実際に残る素材は1番が大理石、2番が青銅(確定)、3番が磁器(確定)、4番オーク(確定)、5番 羊皮紙(確定)。
残った作品は 波、十字、渦巻。これらの条件(3番に波と隣接条件、4番に渦巻の必要性などを当てはめて)を整理すると、手がかり6(十字 と 波 は隣り合う)と手がかり1(大理石 は 渦巻 の左で隣り合わない)を満たす唯一の割り当ては 2番 = 十字、3番 = 波、4番 = 渦巻。1番 は既に 鷹、5番 は 太陽 なので全て埋まる。
以上より最初の「位置ごとの組み合わせ」が一意に決まります。
▶2025年10月の第1週の問題

【問題】
アヤとマコトが家のお手伝いとして、それぞれ同じ枚数の皿洗いと同じ広さの部屋を掃除をすることになりました。
アヤとマコトはまず皿洗いを始めました。
アヤは5分、マコトは15分掛かりましたが、部屋の掃除ではマコトはアヤの半分の時間で手伝いを終えることができました。
2人で3000円のお小遣いをお手伝いの量で分けるとすれば、マコトはいくらもらえるのでしょうか?
【ヒントと答え】
「ヒント1」
3000円をそれぞれのお手伝いの量で分けるということが決まっています。
「ヒント2」
問題文をよく読んで、アヤとマコトのお手伝いの量を考えてみましょう。
「ヒント3」
今分かっているお手伝いの量とは「洗った皿の枚数と掃除した部屋の広さ」です。
【答え】
3000円をそれぞれのお手伝いの量で分けるということが決まっています。
2025年10月期の過去問
▶2025年10月の第1週の問題



【問題】
アヤとマコトが家のお手伝いとして、それぞれ同じ枚数の皿洗いと同じ広さの部屋を掃除をすることになりました。
アヤとマコトはまず皿洗いを始めました。
アヤは5分、マコトは15分掛かりましたが、部屋の掃除ではマコトはアヤの半分の時間で手伝いを終えることができました。
2人で3000円のお小遣いをお手伝いの量で分けるとすれば、マコトはいくらもらえるのでしょうか?
【ヒントと答え】
「ヒント1」
3000円をそれぞれのお手伝いの量で分けるということが決まっています。
「ヒント2」
問題文をよく読んで、アヤとマコトのお手伝いの量を考えてみましょう。
「ヒント3」
今分かっているお手伝いの量とは「洗った皿の枚数と掃除した部屋の広さ」です。
【答え】
当然「1500円」ですね。
▶2025年10月の第2週の問題


【問題】
キャンドルナイトでろうそくが20本燃えていました。
そこへヒュ~っと風が吹き込み、20本の内7本は消えてしまいました。
さらに風が吹き、もう2本消えてしまいました。
これ以上消えないように風よけを作ったところ、
残りのろうそくは1本も消えなかったそうです。
さて最後まで残ったろうそくは何本でしょうか。
【ヒントと答え】
「ヒント1」
一見簡単そうに見える問題ですが、一癖あります。
「最後まで残った」ろうそくの本数ですよ?
「ヒント2」
最初に7本のろうそくが消え、その後に、2本消えてしまったわけです。
つまり火が消えたろうそく本数は?
「ヒント3」
ろうそくが最後まで残る、とはどういうことでしょうか?
ろうそくに火をつけたままにしておくと…
【答え】
そう!もちろん火が消えてしまった「9本」ですね。
▶2025年10月の第3週の問題

【問題】
通販で、とある健康ドリンクを2週間分、14本買いました。
今日から毎日、1日1本ずつ飲まなければならないそうですが、それぞれ効果が異なり、飲む日も決まっているらしいのです。
しかし容器も容量も色も味もまったく同じなので、区別できるように容器に1から通し番号を書くことにしました。
その際、最小で1からいくつまでの数字を書く必要があるのでしょうか。
【ヒントと答え】
「ヒント1」
14本のドリンクに番号をつけるだけであれば1~14までの数字を書けばいいはずですね。
しかし書かなければいけない数字は、14よりも少なくできるはずです。
「ヒント2」
今日から飲みはじめるということは、その1本目に番号は必要ですか?
「ヒント3」
番号が必要ない条件は何でしょうか?
例えば、ドリンクが2本の時は番号が必要ですか?3本になれば?
【答え】
今日の分と最後の日の分(または2日目分)は番号がなくても区別できるので「12」です。
▶2025年10月の第4週の問題


【問題】
スーパーで徳用お菓子を買ってきました。
中には小分けされたチョコが20個入っている袋が3個あります。
これを手づかみでおおよそ1/4ずつに分け、それぞれ袋にラッピングしました。
そして12袋のチョコができたわけです。
このとき、小分けされた袋1つに入っているチョコの数の平均が5個になる確率は何パーセントでしょうか。
【ヒントと答え】
「ヒント1」
チョコが20個入っている大袋が3個あり、チョコは全部で60個あります。
これを12袋に分けるのです。
あとは問題文をよく見直してみましょう。
「ヒント2」
何を答えるのかがポイントです。
チョコの平均が5個になる確率とは?
「ヒント3」
試しに計算してみましょう。
20個の大袋を3個で、チョコの総数は60個ですね。
これを12袋に分けたのなら、1袋あたり5個となりますね。
【答え】
“平均”が5個になる確率なので、答えは「100パーセント」です。
▶2025年10月の第5週の問題


【問題】
使い捨てライターに、一回だけ着火できる量のガスが残っています。
この状況でアルコールランプを灯し、暖炉に火を焚べ、浴槽の水まで沸かして湯につかりたいと思った場合に、まっ先に火をつけるべきは何でしょうか。
【ヒントと答え】
「ヒント1」
もちろん順番は大事ですね。
その中でも、いの一番に火をつけるべきは?
「ヒント2」
まず“これ”に火をつけることが先決です。
これに火をつけなければ、あとは何も出来ません。
「ヒント3」
冷静に考えてみましょう!
【答え】
もちろん「ライター」です。
2025年11月期の過去問
▶2025年11月の第1週の問題


【問題】
スーパーのチラシを見ていると、かなり安くなっている商品がいくつかあるようです。
しかし予算に限りがあるので、チラシの中でも一番安いといえる商品を買いたいのですが、それはどれでしょうか。
A.キャベツ(いつもは284円のところ、半額で142円!)
B.鶏肉(本日割引デー!3割引で166円!)
C.醤油(商品入れ替えにより60%オフの153円!)
D.バナナ(持ってけ泥棒!3房セットで148円!)
【ヒントと答え】
「ヒント1」
できるだけ簡単に考えてみましょう。
いちばん安いといえる商品を選ぶだけですよ?
「ヒント2」
割引率?
いちばん安いものを選んでください。
「ヒント3」
これは引っ掛け問題です。
単純に一番値段の安いものを選べばよいのです。
【答え】
答えはもちろん「A」のキャベツですね。
▶2025年11月の第2週の問題


【問題】
タカシくんは、新しいゲームを買うために家電量販店に行きました。
するとゲーム機本体と新作ソフトが6,5000円で売られていたそうです。
店員さんに聞くと、ゲーム機本体はソフトよりも60,000円高く、残りがソフト代だと言うのです。
幸いゲーム機本体を持っていたタカシくんは、新作ソフトだけを買うことにしました。
レジで10,000円札を出したのですが、お釣りはいくらもらえたでしょうか。
【ヒントと答え】
「ヒント1」
ゲーム機とソフトの値段の合計が65,000円です。
そして、その差額が60,000円だそうです。
「ヒント2」
ソフトをx円としたとき、ゲーム機本体の値段はソフトより60,000円高いので、x+60,000円になります。
つまり、ゲーム機本体は60,000円よりも高いということですね。
「ヒント3」
ゲーム機とソフトで65,000円です。
ゲーム機はソフトより60,000円高いのです。
ゲーム機が60,000円、ソフトが5,000円と考えがちですが、その場合は差額が55,000円なので合いませんね!
【答え】
ソフトが2,500円なので、答えは「7,500円」です。本体に比べれば良心的ですね!
▶2025年11月の第3週の問題


【問題】
友達3人で遊んでいたところ、3人のスマホが皆同じ機種であることに気が付きました。
3人共ケースなどをつけていなかったので、見ただけではまったく区別がつきません。
このような状況で、それぞれが自分のスマホかどうかを確認せずに手に取ったとき、3人の内で2人だけが自分のスマホを取る確率は何パーセントになるでしょうか。
【ヒントと答え】
「ヒント1」
3つのスマホの中から自分のものを手に取る確率を聞かれているわけではありませんよ?
「ヒント2」
2人が自分のスマホを手にしたとき、残りのスマホは誰のものですか?
「ヒント3」
2人だけが自分のスマホを手に取るなんて、そんなことができるでしょうか。
【答え】
答えはもちろん「0パーセント」です。
▶2025年11月の第4週の問題


【問題】
宇宙人が地球人の様子をこっそり観察して、つぶやいています。
「あの道具には、光をよく反射する色素と光をよく吸収する色素が付着した炭素系物質が、ある一定の規則に従い並べられているようだ。さらに、その物質を押し込むことによって大気の振動が発生し、その様々な波長が何とも快いものである。」
さて、いったいなにを見たのでしょう。
【ヒントと答え】
「ヒント1」
身の回りにある見慣れたものも、それを初めてみる人には不思議な道具に見えることがありますね。
「ヒント2」
光をよく反射する色素と光をよく吸収する色素とは、おそらく白色と黒色のことで、炭素系物質は木材を意味しているのでしょう。
つまり、白と黒に着色された木材が並んでいるようです。
「ヒント3」
大気の振動とは「音」。それが様々な波長を奏で、快いとはどういうことでしょうか。
【答え】
宇宙人にも美しい音色が響いたようです。そう、答えは「ピアノ」ですね。
2025年12月期の過去問
▶2025年12月の第1週の問題


【問題】
規則的に並べられたカードにはアルファベットが一文字ずつ書かれているようです。
◯部分に入るアルファベットはなんでしょうか?
…AM◯JA…
【ヒントと答え】
「ヒント1」
規則性がある言葉を色々と考えてみましょう。
「ヒント2」
どうやら問題になっている部分の前後にも言葉が入るようです。
「ヒント3」
問題の前後も合わせて、アルファベットは全部で12個!
周りを見渡せば答えが書いてあるかも?
【答え】
月の英語の頭文字を表していたので、答えは「J」です!
January
February
March
「A」pril
「M」ay
「J」une
「J」uly
「A」ugust
September
October
November
December
あなたは全部書けますか?
▶2025年12月の第2週の問題


【問題】
誰かがいたずらで書いたようなメモを残していきました。
「クッキーを焼いたので、9に6を足した数だけ食べて下さい。」
では、6から5を引いた数が「1」、10に10を足した数が「8」になる時、食べて良いクッキーは何個ですか?
【ヒントと答え】
「ヒント1」
お菓子だけにおかしな計算ですが、決して間違いではありません。
みんなが常日頃から、このような計算をしています。
「ヒント2」
6から5を引いて1になるのは当然ですが、10に10を足して8になるものはなんでしょう?
身の回りにある、ある道具を見たときに、この計算をすることがあるようです。
「ヒント3」
この計算では、足し算で12までしか数が増えないようですが、
最近では、24まで計算する方法もよく見ますね。
【答え】
時計を見て問題を考えたようです。答えは「3」個ですね。
▶2025年12月の第3週の問題


【問題】
父と母が異なるお小遣いの条件で手伝いを要求してきました。
お小遣い以外は同じ内容の時、どちら条件で手伝うのがお得でしょうか?
父の条件、時給300円。
最初の1時間以降は1時間ごとに時給が100円ずつ増えます。
母の条件、30分給150円。
最初の30分以降は30分ごとに30分給が25円ずつ増えます。
【ヒントと答え】
「ヒント1」
難しく考えずに計算してみましょう。
1時間ごとのお小遣いはどうなりましたか?
「ヒント2」
父の方は時給なので、1時間ごとにもらえる額ですね。
母の方は30分給なので、30分ごとにお小遣いがもらえることになります。
「ヒント3」
ヒント1での計算が答えになります。
父のお小遣いは300円。
母の方は最初の30分で150円、そこから25円昇給して、残りの30分は175円。その合計は?
【答え】
一時間目のお小遣いは、父300円、母325円。
二時間目のお小遣いは、父400円、母425円。
細かい数字だけ見ると母は少なく見えますが、一時間ごとのおこづかいは常に母が多くなります。
手伝うとお得なのは「母」でした。
▶2025年12月の第4週の問題


【問題】
3つの普通のサイコロを1回ふった時に、ゾロ目が出る確率は、36分の1です。
もし2回連続でゾロ目が出たとすれば、それは1296分の1の確率であり、さらに3回連続で出た場合は46656分の1というとんでもない確率になります。
では、3つの普通のサイコロを3回ふって3回ともゾロ目が出てしまったとすれば、次にふる4回目にゾロ目が出る確率は一体何分の1になってしまうのでしょうか。
【ヒントと答え】
「ヒント1」
じっくり考えてみましょう。
「ヒント2」
46656に36をかけてみる…必要はありません。
「ヒント3」
今からふるサイコロの目がゾロ目になる確率をきかれています。
【答え】
答えは当然「36」ですね。
2026年1月期の過去問
▶2026年1月の第1週の問題


【問題】
とあるフェリーが氷山に激突してしまい、直に沈没してしまいそうです。
そのフェリーには乗組員含め20人の人が乗船しています。
この辺りの海は水温が低く、泳いでの避難は不可能とのこと。
ですが、幸いにも定員4人の救命ボートが1隻あり、近くの港に避難できるそうです。
フェリーから港まで往復2分かかる場合、全員救助するまでに何分必要でしょうか。
【ヒントと答え】
「ヒント1」
往復2分は救命ボートへの乗り降りを含めた時間です。
「ヒント2」
最初の救命ボートが4人を乗せて出発してから2分後には、次の救命ボートがまた人を乗せて出発できるということです。
「ヒント3」
定員4人のボートなので最初は4人乗せられますが、それ以降は…。
【答え】
操舵手が1人必要なので、2回目以降は3人ずつ乗せられます。計算すると、
残り20人→4人を乗せて、2分経過→
残り16人→3人乗せて、4分経過→
残り13人→3人乗せて、6分経過→
残り10人→3人乗せて、8分経過→
残り7人→3人乗せて、10分経過→
残り4人→3人乗せて、12分経過→
残り1人→1人乗せて、フェリーに戻る必要はないので片道1分後港へ
答えは「13分」でした。
▶2026年1月の第2週の問題

【問題】
ここはとある研究所。実験中のシャーレの中に10個の細菌がいる。
この細菌は三十秒後に5個に減るが、一分後には20個に分裂するという。
分裂した20個は、また30十秒後に10個まで減り、一分後に40個に分裂する。
では、実験開始時に10個だった細菌は5分30秒後に何個になる?
【ヒントと答え】
「ヒント1」
三十秒で10個が5個に減り、一分後に20個まで増える。
以降は同じ計算を一分毎に繰り返す。
「ヒント2」
内容としては単純な計算である。
「ヒント3」
一分毎で見れば倍になっていくだけだが、三十秒間隔で見れば話は異なる。
【答え】
計算方法は
10個×2⁵(←五分後の細菌の数)÷2(三十秒で半減)=160個
答えは「160個」だ。
▶2026年1月の第3週の問題


【問題】
とある地方に競馬場があります。そのコースを30秒で走る距離は、以下の通りだそうです。
馬Aは0.5周
馬Bは1周
馬Cは2周
スタートラインからABCの三頭が同方向に同時に走り出したとすると、再びスタートラインで三頭が並ぶのは最短何分後でしょうか。
【ヒントと答え】
「ヒント1」
問題をよく読んで、考えてみましょう。
「ヒント2」
馬たちは、それぞれ走る速さが異なります。
しかし、「1分間」にコースを何週できるか、は簡単に求められそうですね。
「ヒント3」
1分間走り終えた馬たちは、どこにいるのでしょうか。
【答え】
一番遅い馬Aが最短1分でスタートラインに戻るので、そこで2周走った馬B、4周走った馬Cと並びます。
つまり答えは「1分後」ですね。
スライドパズルもどうぞ
「赤い玉」と「緑の玉」の位置を入れ替えよう!